相关文档
第1套人教初中数学八上 15.3 分式方程(第1课时)分式方程课件 【通用,最新经典教案】










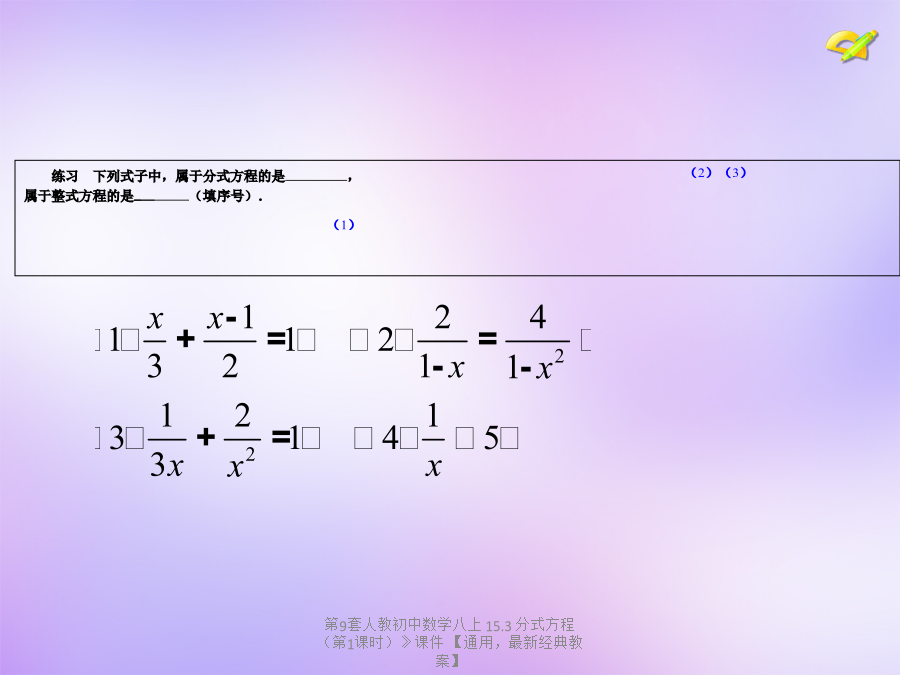
第9套人教初中数学八上 15.3 分式方程(第1课时)》课件 【通用,最新经典教案】










第1套人教初中数学八上-15.3-分式方程(第1课时)分式方程课件-【通用-最新经典教案】










第9套人教初中数学八上 15.3 分式方程课件1 【通用,最新经典教案】










第1套人教初中数学八上 15.3 分式方程(第2课时)分式方程的应用课件 【通用,最新经典教案】










第2套人教初中数学八上 15.3 分式方程课件 【通用,最新经典教案】










第9套人教初中数学八上 15.3 分式方程(第3课时)》课件 【通用,最新经典教案】










第9套人教初中数学八上 15.3 分式方程(第2课时)》课件 【通用,最新经典教案】










第9套人教初中数学八上 15.3 分式方程课件3 【通用,最新经典教案】










第9套人教初中数学八上 15.3 分式方程课件2 【通用,最新经典教案】










最新文档